Мы считаем, что эта тема достаточно
актуальна.
Ведь многие учёные ломали голову, чтобы
решить Великую теорему Ферма, а решения выходили то с ошибкой, то на несколько
сотен страниц. Говорят, будто сам Ферма не смог доказать эту теорему, а доказал
лишь для частных случаев.
Малая же теорема широко используется при
решении математических задач по теме «Теория чисел».
Теорема
Ферма.
Большая теорема Ферма.
Вели́кая теоре́ма
Ферма́ (или Последняя теорема Ферма) —
одна из самых популярных теорем математики. Её условие формулируется
на понятийном уровне среднего общего образования, а доказательство теоремы
искали многие математики более трёхсот лет. Окончательно доказана в 1994 году Эндрю Уайлсом.
Теорема утверждает, что:
Для
любого натурального числа

не имеет решений в целых ненулевых
числах
|
Встречается
более узкий вариант формулировки, утверждающий, что это уравнение не
имеет натуральных решений. Однако очевидно, что если
существует решение для целых чисел, то существует и решение в натуральных
числах. В самом деле, пусть  — целые
числа, дающие решение уравнения Ферма. Если
— целые
числа, дающие решение уравнения Ферма. Если  чётно,
то
чётно,
то  тоже
будут решением, а если нечётно, то перенесём все степени отрицательных значений
в другую часть уравнения, изменив знак. Например, если бы существовало решение
уравнения
тоже
будут решением, а если нечётно, то перенесём все степени отрицательных значений
в другую часть уравнения, изменив знак. Например, если бы существовало решение
уравнения 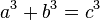 и при
этом
и при
этом
отрицательно,
а прочие положительны, то  ,, и
получаем натуральные решения
,, и
получаем натуральные решения  Поэтому обе формулировки эквивалентны.
Поэтому обе формулировки эквивалентны.
 — целые
числа, дающие решение уравнения Ферма. Если
— целые
числа, дающие решение уравнения Ферма. Если  чётно,
то
чётно,
то  тоже
будут решением, а если нечётно, то перенесём все степени отрицательных значений
в другую часть уравнения, изменив знак. Например, если бы существовало решение
уравнения
тоже
будут решением, а если нечётно, то перенесём все степени отрицательных значений
в другую часть уравнения, изменив знак. Например, если бы существовало решение
уравнения 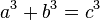 и при
этом
и при
этом  ,, и
получаем натуральные решения
,, и
получаем натуральные решения  Поэтому обе формулировки эквивалентны.
Поэтому обе формулировки эквивалентны.
Для случая 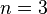 эту
теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не
сохранилось.
эту
теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не
сохранилось.
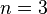 эту
теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не
сохранилось.
эту
теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не
сохранилось.
В общем виде теорема была
сформулирована Пьером Ферма в 1637 году на
полях «Арифметики» Диофанта. Дело в
том, что Ферма делал свои пометки на полях читаемых математических трактатов и
там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой
ведётся речь, он записал с припиской, что найденное им остроумное
доказательство этой теоремы слишком длинно, чтобы его можно было поместить на
полях книги:
Наоборот,
невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще
никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел
этому поистине чудесное доказательство, но поля книги слишком узки для него.
Несколько позже сам Ферма опубликовал доказательство частного случая для  , что добавляет сомнений в том, что у него было доказательство общего случая.
, что добавляет сомнений в том, что у него было доказательство общего случая.
 , что добавляет сомнений в том, что у него было доказательство общего случая.
, что добавляет сомнений в том, что у него было доказательство общего случая.
Эйлер в 1770 году доказал теорему для случая 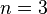 , Дирихле и Лежандр в 1825 — для
, Дирихле и Лежандр в 1825 — для  , Ламе — для
, Ламе — для 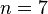 . Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.
. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.
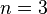 , Дирихле и Лежандр в 1825 — для
, Дирихле и Лежандр в 1825 — для  , Ламе — для
, Ламе — для 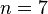 . Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.
. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.
Над полным доказательством Великой
теоремы работало немало выдающихся математиков и множество
дилетантов-любителей; считается, что теорема стоит на первом месте по
количеству некорректных «доказательств». Тем не менее эти усилия привели к
получению многих важных результатов современной теории чисел. Давид Гильберт в
своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме:
Проблема
доказательства этой неразрешимости являет разительный пример того, какое
побуждающее влияние на науку может оказать специальная и на первый взгляд
малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл
к введению идеальных чисел и к
открытию теоремы об однозначном разложении чисел в круговых полях на
идеальные простые множители — теоремы, которая теперь, благодаря
обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является
центральной в современной теории чисел и значение которой выходит далеко за
пределы теории чисел в область алгебры и теории функций.
В 1908 году немецкий любитель математики
Вольфскель завещал 100 000 немецких марок тому,
кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.
В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение 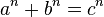 при
при  может иметь лишь конечное число взаимно простых решений.
может иметь лишь конечное число взаимно простых решений.
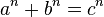 при
при  может иметь лишь конечное число взаимно простых решений.
может иметь лишь конечное число взаимно простых решений.
Последний, но самый важный, шаг в
доказательстве теоремы был сделан Уайлсом в сентябре 1994 года. Его
130-страничное доказательство было опубликовано в журнале «Annals of Mathematics». Доказательство
основано на предположении немецкого математика Герхарда Фрая о том, что Великая
теорема Ферма является следствием гипотезы Таниямы — Симуры (это
предположение было доказано Кеном Рибетом при участии Ж.‑П. Серра).
Первый вариант своего доказательства
Уайлс опубликовал в 1993 году (после
7 лет напряжённой работы), но в нём вскоре был обнаружен серьёзный пробел,
который с помощью Ричарда Лоуренса Тейлора удалось
достаточно быстро устранить. В 1995 году был опубликован завершающий
вариант.
Простота формулировки теоремы Ферма
(доступная в понимании даже школьнику), а также сложность единственного
известного доказательства (или неведение о его существовании), вдохновляют
многих на попытки найти другое, более простое, доказательство. Людей,
пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами»
или «ферматиками».Ферматисты зачастую не владеют основами математической
культуры и допускают ошибки в арифметических действиях или логических выводах, хотя
некоторые представляют весьма изощрённые «доказательства», в которых трудно найти
ошибку.
Доказывать теорему Ферма в среде
любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя
статью о теореме Ферма, сопроводил ее следующей припиской:
Редакция «Кванта» со своей стороны считает
необходимым известить читателей, что письма с проектами доказательств теоремы
Ферма рассматриваться (и возвращаться) не будут.
|
Немецкому математику Эдмунду Ландау очень докучали
«ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот
бланков со следующим текстом:
Уважаемый …! Благодарю Вас за присланную Вами
рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на
стр. … в строке …
|
Находить ошибку и заполнять пробелы
в бланке он поручал своим аспирантам.
Примечательно, что отдельные
ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной
прессе, которая раздувает их значение до научной сенсации. Впрочем,
иногда такие публикации появляются и в уважаемых научных изданиях, как правило,
с последующими опровержениями. Среди других примеров:
·
Брошюра В. И. Будкина, изданная в Ярославле
под названием «Методика познания „истины“. Доказательство Великой теоремы
Ферма» (47 стр., 5000 экз., Верхне-Волжское книжное издательство, 1975).
·
Книга Л. Ш. Райхеля «Великая теорема»,
изданная в Ленинграде в 1990 году.
Свидетельство о регистрации авторских прав на
произведение «доказательство теоремы Ферма», выданное Министерством образования
и науки Украины Л. В. Шаповаловой и Г. А. Середкину.
Следует пояснить, что этот документ не удостоверяет каким-либо образом
правильность доказательства, а лишь регистрирует авторские права на поданный в
Министерство образования и науки печатный труд; на это министерство возложена
обязанность ведения реестра таких свидетельств.
Великая теорема Ферма стала символом
труднейшей научной проблемы и в этом качестве часто упоминается в
беллетристике. Далее перечислены некоторые произведения, в которых теорема не
просто упомянута, но является существенной частью сюжета или идеологии
произведения.
·
В повести Е. Велтистова «Победитель невозможного» друг Сыроежкина и
Электроника Вова Корольков в качестве свободного задания по математике доказал
Великую теорему Ферма.
·
В телесериале «Звёздный Путь», капитан
космического корабля Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма
во второй половине XXIV века. Таким образом, создатели фильма
предполагали, что решения у Великой теоремы Ферма не будет в ближайшие 400 лет.
Серия «Рояль» с этим эпизодом была снята в 1989 году, когда Эндрю Уайлс был в
самом начале своих работ. В действительности решение было найдено всего спустя
5 лет.
·
В рассказе Артура Порджеса «Саймон Флэгг и дьявол» профессор
Саймон Флегг обращается за доказательством теоремы к дьяволу. По этому рассказу
снят игровой научно-популярный фильм «Математик и чёрт» (СССР, 1972, производство Центрнаучфильм, творческое объединение «Радуга»,
режиссёр Райтбурт).
·
В рассказе Кира Булычева «Мечта
заочника» студент-заочник Гаврилов приходит к профессору Минцу и приносит
купленную курсовую работу, в которой приводится доказательство теоремы, с
просьбой объяснить, что он написал.
·
В посвящённой Хэллоуину 1995 года серии «Симпсонов» двумерный Гомер Симпсон
случайно попадает в третье измерение. Во время его путешествия в этом странном
мире, в воздухе парят геометрические тела и математические формулы, включая
равенство  .
Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:
.
Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:
 .
Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:
.
Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:
178212 + 184112 =
2541210258614589176288669958142428526657 ≈ 254121026·1031
192212 =
2541210259314801410819278649643651567616 ≈ 254121026·1031
Тем не менее, даже без вычисления
точных значений легко видеть, что равенство неверно: левая часть — нечётное число, а правая
часть — чётное.
·
В первом издании «Искусства
программирования» Дональда Кнута теорема
Ферма приведена в качестве упражнения с математическим уклоном в самом начале
книги и оценена максимальным числом (50) баллов, как «исследовательская
проблема, которая (насколько это было известно автору в момент написания) ещё
не получила удовлетворительного решения. Если читатель найдет решение этой
задачи, его настоятельно просят опубликовать его; кроме того, автор данной
книги будет очень признателен, если ему сообщат решение как можно быстрее (при
условии, что оно правильно)». В третьем издании книги это упражнение
уже требует знаний высшей математики и
оценивается лишь в 45 баллов.
·
В книге Стига Ларссона «Девушка, которая играла с огнём» главная героиня Лисбет Саландер, обладающая
редкими способностями к аналитике и фотографической памятью, в качестве хобби
занята доказательством Великой теоремы Ферма, на которую она наткнулась, читая
фундаментальный труд «Измерения в математике», в котором приводится и
доказательство Эндрю Уайлса. Лисбет не хочет изучать готовое доказательство, а
главным интересом становится поиск собственного решения. Поэтому всё своё
свободное время она посвящает самостоятельному поиску «замечательного
доказательства» теоремы великого француза, но раз за разом заходит в тупик. В
конце книги Лисбет находит доказательство, которое не только совершенно отлично
от предложенного Уайлсом, но и является настолько простым, что сам Ферма мог бы
его найти. Однако, после ранения в голову она его забывает, и Ларссон не
приводит никаких подробностей этого доказательства.
·
Мюзикл «Последнее танго Ферма», изданный институтом
Клэя, создан
в 2000 году Дж. Розенблумом и Дж.
С. Лессер по мотивам реальной истории Эндрю Уайлса. Главный герой по имени
Дэниел Кин завершает доказательство теоремы, а дух самого Ферма старается ему
помешать.
·
За несколько дней до своей смерти Артур Кларк успел
отрецензировать рукопись романа «Последняя Теорема», над которой он трудился в
соавторстве с Фредериком Полом. Книга
вышла уже после смерти Кларка.
·
В рассказе Натальи Дарьяловой «Великая и загадочная»
сюжет строится на теореме Ферма. Рассказывается о том, как молодой человек,
будучи студентом, занялся теоремой Ферма, впоследствии стал математиком,
получил несколько важных научных результатов, но совершенно загубил свою личную
жизнь.
·
В романе П. А. Загребельного «Разгон» скромный
преподаватель математики из Одессы сумел доказать теорему, через некоторое
время стал академиком и возглавил очень серьезное киевское НПО, занимающееся созданием электронно-вычислительных систем.
А. П. Казанцев в романе «Острее шпаги» в 1983
году предложил оригинальную версию отсутствия доказательства самого Пьера
Ферма.
Малая теорема Ферма.
Ма́лая теоре́ма Ферма́ — теорема теории чисел, которая утверждает, что
|
Другими словами:
|
К примеру, если  то
то  и
и 
 то
то  и
и 
Малая теорема Ферма является частным
случаем теоремы
Эйлера, которая, в
свою очередь, является частным случаем теорем Кармайкла и Лагранжа для конечных циклических групп. Теорему
высказал без доказательства Пьер Ферма, первое
доказательство дали Леонард Эйлер и Готфрид
Вильгельм Лейбниц.
Малая теорема Ферма уже давно стала
одной из главных теорем для исследований не только в теории целых чисел, но и в
более широких областях.
Пьер Ферма сформулировал
исходное утверждение теоремы около 1636 года. Письмо от 18 октября 1640 года Пьера
Ферма к французскому математику Бернару Френиклю (Bernard Frénicle de Bessy)
содержало следующее положение:
Каждое простое число делит [в оригинале — «измеряет»] одну из степеней
любой прогрессии минус 1, для которой показатель степени является делителем
данного простого числа минус 1; и после того, как была найдена первая степень,
удовлетворяющая этому свойству, все числа, имеющие показатели степени, кратные
показателю первой, удовлетворяют тому же свойству.
В качестве примера Ферма приводит
прогрессию 3, 9, 27, 81, 243, 729… и простое число 13. 13 делит 27 − 1
(показатель степени для 27 равен 3, а 3 делит 13 − 1), из чего следует, что 13
также делит 729 − 1 (показатель степени для 729 равен 6 и кратен 3).
Ещё в древности китайским математикам была известна гипотеза (иногда называемая «китайской гипотезой»), что если  является простым числом, то
является простым числом, то  (фактически, частный случай малой теоремы Ферма)[4]. Тем не менее, обратное утверждение (о том, что из
(фактически, частный случай малой теоремы Ферма)[4]. Тем не менее, обратное утверждение (о том, что из  следует, что
следует, что  простое), а, следовательно, и гипотеза в целом, оказались неверными
простое), а, следовательно, и гипотеза в целом, оказались неверными
 является простым числом, то
является простым числом, то  (фактически, частный случай малой теоремы Ферма)[4]. Тем не менее, обратное утверждение (о том, что из
(фактически, частный случай малой теоремы Ферма)[4]. Тем не менее, обратное утверждение (о том, что из  следует, что
следует, что  простое), а, следовательно, и гипотеза в целом, оказались неверными
простое), а, следовательно, и гипотеза в целом, оказались неверными
Существует также предположение, что
китайская гипотеза была выдвинута примерно за 2000 лет до аналогичных работ
Ферма. Стоит отметить, что гипотеза могла быть известна и другим математикам
древности, даже несмотря на то, что она оказалась частично неверной. Тем не
менее, в некоторых источниках утверждается, что предположение относительно
столь раннего появления гипотезы является распространённым заблуждением, а в
действительности гипотеза была выдвинута лишь в 1872 году.
Сам Ферма оставил свою теорему без
доказательства. Первым, кому удалось его найти, был Готфрид
Вильгельм Лейбниц, в рукописях которого утверждается, что
доказательство ему было известно до 1683 года. Лейбниц не знал о результате Ферма
и открыл теорему независимо. Но работа Лейбница не была опубликована, и
доказательство (очень похожее) в 1736 году обнародовал Эйлер в
статье Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio.
Доказательство малой теоремы Ферма, основанное на том, что целые числа
сравнимы
в некотором порядке с числами
, было
опубликовано в 1806 году Джеймсом
Айвори.
Одно из самых простых, но наименее
элементарных доказательств Малой теоремы Ферма основано на следствии теоремы Лагранжа из теории групп,
утверждающей, что порядок элемента конечной группы делит порядок группы.
Напомним, что порядком конечной группы  называется число её элементов, а порядком элемента
называется число её элементов, а порядком элемента 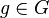 — наименьший показатель его степени, равной единичному элементу
— наименьший показатель его степени, равной единичному элементу  группы
группы  .
.
 называется число её элементов, а порядком элемента
называется число её элементов, а порядком элемента 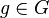 — наименьший показатель его степени, равной единичному элементу
— наименьший показатель его степени, равной единичному элементу  группы
группы  .
.
Пусть  — конечная группа порядка
— конечная группа порядка  . Из того, что порядок элемента
. Из того, что порядок элемента 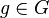 делит
делит  , следует, что
, следует, что  .
.
 — конечная группа порядка
— конечная группа порядка  . Из того, что порядок элемента
. Из того, что порядок элемента 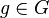 делит
делит  , следует, что
, следует, что  .
.
Рассмотрим поле 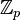 вычетов по модулю
вычетов по модулю  . Вычет целого числа
. Вычет целого числа  будем обозначать через
будем обозначать через  . Ненулевые элементы поля
. Ненулевые элементы поля 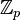 образуют группу относительно умножения.
образуют группу относительно умножения.
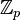 вычетов по модулю
вычетов по модулю  . Вычет целого числа
. Вычет целого числа  будем обозначать через
будем обозначать через  . Ненулевые элементы поля
. Ненулевые элементы поля 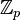 образуют группу относительно умножения.
образуют группу относительно умножения.
Порядок этой группы, очевидно, равен  . Её единичным элементом является
. Её единичным элементом является  . Отсюда следует, что для каждого числа
. Отсюда следует, что для каждого числа  , не делящегося на
, не делящегося на  ,
,  , но это как раз означает сравнение
, но это как раз означает сравнение 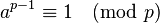
 . Её единичным элементом является
. Её единичным элементом является  . Отсюда следует, что для каждого числа
. Отсюда следует, что для каждого числа  , не делящегося на
, не делящегося на  ,
,  , но это как раз означает сравнение
, но это как раз означает сравнение 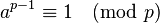
Докажем малую теорему Ферма в другой
формулировке.
Если целое число  не кратно простому числу
не кратно простому числу  , то
, то  даёт остаток 1 при делении на
даёт остаток 1 при делении на  .
.
Лемма: Для любого простого числа  и целого числа
и целого числа  , не кратного
, не кратного  , произведения
, произведения  и чисел
и чисел  при делении на
при делении на  дают те же самые числа
дают те же самые числа  возможно, записанные в некотором другом порядке
возможно, записанные в некотором другом порядке
 и целого числа
и целого числа  , не кратного
, не кратного  , произведения
, произведения  и чисел
и чисел  при делении на
при делении на  дают те же самые числа
дают те же самые числа  возможно, записанные в некотором другом порядке
возможно, записанные в некотором другом порядке
Докажем её:
Произведение  и любого из чисел и любого из чисел  не кратно не кратно  , следовательно, в остатке не может получиться , следовательно, в остатке не может получиться  . Все остатки разные. Докажем последнее утверждение от противного. Пусть два произведения . Все остатки разные. Докажем последнее утверждение от противного. Пусть два произведения  и и  дают при делении на дают при делении на  одинаковые остатки, тогда разность одинаковые остатки, тогда разность  кратна кратна  , что невозможно, поскольку , что невозможно, поскольку  не кратно не кратно  . Всего существует . Всего существует  различных ненулевых остатков от деления на различных ненулевых остатков от деления на  . .Поскольку согласно выше приведенной лемме остатки от деления чисел a, 2a, 3a, ..., (p − 1)a — это с точностью до перестановки числа 1, 2, 3, ..., p − 1, то  . Отсюда . Отсюда  . Последнее соотношение можно сократить на(p − 1)!, поскольку все сомножители являются числами, взаимно простыми с основанием p, в результате получаем требуемое утверждение . Последнее соотношение можно сократить на(p − 1)!, поскольку все сомножители являются числами, взаимно простыми с основанием p, в результате получаем требуемое утверждение 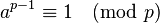 А теперь мы предлагаем Вам решить задачу с помощью малой теоремы Ферма. |
Задача
Какой остаток даёт число 3100
при делении на 101?
Решение
Как мы знаем из теоремы если  — простое и
— простое и  — целое число, не делящееся на
— целое число, не делящееся на  , то,
, то,  делится на
делится на  , то есть
, то есть 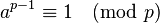 .
.
 — простое и
— простое и  — целое число, не делящееся на
— целое число, не делящееся на  , то,
, то,  делится на
делится на  , то есть
, то есть 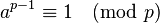 .
.
Мы знаем, что 101 - простое, а - целое число, не делящееся на 101, то есть все условия соблюдены и мы можем применить эту теорему.
Следовательно, число 3100 даёт остаток 1, при делении на 101.
Ответ: 1.
 при делении нацело на
при делении нацело на
Познавательно 9/10
ОтветитьУдалитьВаш Проэкточень интересен. Все расписано и понятно, ваша информация Очень познавательна. Желаю успехов в последующих начинаниях!
ОтветитьУдалитьИнтересная тема, но, по-моему, слишком много не нужной информации. А так, очень хороший блог. Молодцы!:)
ОтветитьУдалитьИнтересная тема !!! Благодаря вам я узнала очень много о Большой теореме Ферма ! Мой совет поменяйте фон на белый , тогда читать станет легче !
ОтветитьУдалитьВаш покорный фанат номер 1(дэ ))))))!)))))
ЙА НАЧИНАЮЩИЙ БЛОГИР! ПАТПИШИСЬ НА МЕНЯ. У МЕНЯ ТОЖИ ОЧЕНЬ МНОГО ПРО ТИОРЕМУ ФИРМА! КАЖДЫЙ МЕСИЦ КОНКУРС!
ОтветитьУдалить"Терма Ферма - основа нашей жизни" говорил мой дед!
ОтветитьУдалитьВеликолепно